CONTACT

时间:2024-05-26 10:00:10 点击量:
当我们说AI算法,现在也基本在说深度学习了,而当前主流的深度学习算法是基于梯度算法的,易陷入局部最优,而且无法解决不可微的问题,而进化算法是不需要梯度能跳出局部优的黑箱算法,但是面对高纬空间效率低,业界也有把进化梯度结合起来的趋势。
用AI算法解决问题本质上是一个优化问题,问题维度高,解空间巨大。国内有很强优化理论基础的老师已经在从优化角度出发,看深度学习的问题,比如北大林宙辰老师,推荐[1][2]两篇paper。
[1]:Optimization Algorithm Inspired Deep Neural Structure Design
优化算法启发设计更好的深度网络架构.
[2]:Lifted Proximal Operator Machines
把DNN的训练(多凸深层嵌套函数的优化)转换为带约束的优化问题(解嵌套了更好分析,可以用更高效的方式优化),把约束条件加入到loss作为惩罚项,去逼近原来的解.
这里希望各路大神发表下观点~~~,优化理论究竟会怎样帮助到深度学习呢?有没有什么根本性的改进或者改变?
这系列文章最早的
Learning fast approximations of sparse coding
K Gregor , Y Lecun icml2010
对于dictionary有相关性的压缩感知的问题dl能带来的benefit
Bo Xin, Yizhou Wang, Wen Gao, Baoyuan Wang, and David Wipf, "Maximal Sparsity with Deep Networks?," Advances in Neural Information Processing Systems (NIPS), 2016
Hao He, Bo Xin, Satoshi Ikehata, and David Wipf, "From Bayesian Sparsity to Gated Recurrent Nets," Advances in Neural Information Processing Systems (NIPS), 2017.
在图像处理的应用
Deep ADMM-Net for compressive sensing MRI(nips16?,pami版本改了frank Wolfe做了一个net)
收敛的保障
Xiaohan Chen*, Jialin Liu*, Zhangyang Wang, Wotao Yin. “Theoretical Linear Convergence of Unfolded ISTA and its Practical Weights and Thresholds.” Advances in Neural Information Processing Systems (NIPS), 2018
arXiv:1808.05331[pdf, other]cs.CV
On the Convergence of Learning-based Iterative Methods for Nonconvex Inverse Problems
Risheng Liu, Shichao Cheng, Yi He, Xin Fan, Zhouchen Lin, Zhongxuan Luo
在assumption很强【很简单的任务】上 learning没有必要 手动设计weight可以optimal
Jialin Liu*, Xiaohan Chen*, Zhangyang Wang, Wotao Yin. “ALISTA: Analytic Weights Are As Good As Learned Weights in LISTA.” In Proceedings of International Conference on Learning Representations (ICLR), 2019
包括如果考虑下weijie su老师的
su,boyd,candes A Differential Equation for Modeling Nesterov's Accelerated Gradient Method: Theory and Insights
这个和最近火的neural ode也是一样的思路
Yiping Lu, Aoxiao Zhong, Quanzheng Li, Bin Dong. "Beyond Finite Layer Neural Network:Bridging Deep Architects and Numerical Differential Equations" Thirty-fifth International Conference on Machine Learning (ICML), 2018
控制 优化 dl应该联系很深
用控制角度看优化
L. Lessard, B. Recht, and A. Packard. Analysis and design of optimization algorithms via integral quadratic constraints. SIAM Journal on Optimization, 26(1):57–95, 2016.
就是优化是最特殊的梯度流,dl和控制里很多问题都可能不是梯度流
既然被邀请,就说说自己的想法。先说明一下,我接触的这方面的论文不多,所以只是按照自己的理解来谈。
深度神经网络的结构的功能,在目前应该包括两个部分,一个是用来编码问题的解,就是拟合一个目标函数,网络结构定义了我们认为的解空间;第二个是提供信息流动的通路,包括前向的计算和后向的误差传递通路,实际上这个通路部分在这里我更愿意强调后向的部分,因为前向通路实际上可以认为属于结构的第一部分功能。在目前最通用的CNN结构中,前向和后向共享一个结构,前向数据流和后向数据流在一个结构上流动,只不过方向不同而已。
对于我个人而言,我更关心前向编码的部分,因为这是我认为和物理联系更紧密的部分,也是更根本的部分,大自然是不需要后向信息流的。但是我们人类必须要考虑数据驱动的网络训练,那么这样一来后向部分同样重要,甚至对于应用而言可能更加重要(我们有时候只关心能不能用,不太关心前向的编码是不是高效或者最优),这应该就是这个问题的核心。
如果从问题来看,我认为主要的目标就是如何改变后向通路,就是如何可以构建网络使得后向的通路可以和前向通路分离或者至少不被前向通路限制。这一点实际上早就有这个想法,比如Hinton以前就提过可以不被BP限定,哪怕随机BP也可以完成较好的优化。我想,这个方向利用优化思想来改善网络结构设计就是要让后向信息流更灵活多变,这个后向通路可以参考现有的优化方法来进行设计,这一点是自然的。
在前向后向之间还有一个中间地带,就是二者有时候是耦合的,比如采用自控思路的方法,就是把一部分前向的结构约束变成优化代价函数的一部分,这个就是最近NDE一类的采用adjoint calculation的思路,实际上就是把前向后向耦合起来了,让后向完成部分前向的功能,这时候其实前向和后向的通路就已经分离为两个,但是二者是耦合的而非独立的。
所以,一般而言,前向和后向应该是可以分离的,原有的DN是不分离的,而且是前向占据统治地位,后向被前向限定,后来逐渐出现二者耦合,把部分的前向功能让后向来完成,加重了后向的比重,现在这个问题可能就是要更加解放后向,让其完全与前向脱离。
需要说明一点,这个思路的重点在训练网络而不是前向编码,所以对于我个人的观点而言,这更多是为了解决应用问题而采取的策略,应该不是深度网络思想本身的核心部分,正如我们的科学更看重我们总结出的前向的推导出世界运行规律的部分,我们更看重这个结构的优化和美,我们知道这个前向的规则是有好的结构的并且努力寻找这个结构,而对于如何从观测结果来反向的得到这个规律的过程的结构相对忽略,或者说很难对这个逆向过程总结出规律。有可能这个逆向过程本身就没有好的结构,我们只能是迁移一下已有的经验。所以我们的课本都是教授我们前向的规则,很少能告诉我们逆向的规则,都是靠自己摸索。
我个人是对是否可以把优化的部分独立出来考察是有点存疑的(不是说前后向不可以分开考虑,但是分开独立考虑可能不会是最佳的方案)。如果说网络结构和数据自身的信息模式之间应该耦合,那么所谓优化就是寻找这个最佳的耦合点,所以优化(或者最佳优化方法)应该也是和网络结构以及数据结构耦合的,所以在对数据结构特征不了解的情况下试图直接通过优化方法的选择来改善系统性能,其一般通用性或者有效性,我是持谨慎态度的。大概是,我们可以这么做,这种方法在某些系统上似乎也会更加有效,但是这种将前后向独立考察的思路,或者说要么是原来的用前向来限定后向,或者是这里的从后向来限定前向,都可能不会是最佳方案。
谢 @我是黑猫警长的幺崽崽 邀。这个问题和深度学习如何影响运筹学?这个问题比较相关,两者自然是互相影响的。现在学界的现状就是不少CS的学者也在做优化,不少传统做优化的也开始做机器学习/深度学习理论了(learning theory)。
要探讨这个问题,我肯定姿势水平不够,而自然是要在学界浸润多年的大佬才有资格。我这边就主要引用一下2018年初L′eon Bottou,Frank E. Curtis, Jorge Nocedal的观点。也算是他们这篇著名的review paper的一个导读了。
其中,L′eon Bottou是Facebook AI实验室(FAIR)著名的深度学习专家(惊艳的Wasserstein GAN就出于他手),Jorge Nocedal是优化界巨擎,2017年冯·诺依曼奖获得者(运筹学/优化界最高的理论奖项),Frank E. Curtis的资历比起来要稍微逊色一些,是Lehigh大学的教授。
来源:Bottou L, Curtis F E, Nocedal J. Optimization methods for large-scale machine learning[J]. SIAM Review, 2018, 60(2): 223-311.
我们知道,无论是机器学习还是深度学习算法,其支柱(pillar)之一便是数学优化(mathematical optimization)。具体来说,我们的学习算法(learning algorithm)需要根据数据集(data)训练(train)出一组最优(optimal)的参数(parameters)。而目前这个时代,深度学习,或者说超大规模的机器学习带来了一类新的问题情境,使得传统的非线性/数值优化算法无法直接被使用。
这里我们考虑如下三个问题:
对第一个问题,文中举了两个实际案例(case studies)来笼统回答。一个是基于传统凸优化(convex optimization)方法(逻辑回归,支持向量机)就能完成的语义分类(text classification)实例。而第二个实例则是所谓的认知任务(perceptual tasks),比如语音和图像识别(speech and image recognition)。这类问题,目前的工业界实践发现基于深度神经网络(deep neural nets, DNN)的算法模型可以得到比传统的机器学习算法好得多的训练效果。而这类问题所对应的大规模优化问题是高度非凸(nonconvex)和非线性(nonlinear)的,这是目前传统运筹学领域无法解决的一类优化问题。
第二个问题(包括第三个问题的前半部分),目前深度学习使得一类传统的梯度下降类算法(gradient based algorithm)显得落实了,因为它们对于梯度的迭代更新都是in batch(一波一起更新)的。与此相对的,Robbins and Monro半个多世纪以前提出的随机梯度方法(stochastic gradient method, SG)反而引起了强烈的研究兴趣。这里,文章讨论了最近一些基于SG的新优化算法。总的来说,这些新算法具有适合大规模机器学习问题的三大特性:
Open question就多了。别的不论,如何针对各类深度学习问题找到更快/精度更高的优化算法,这应该会是之后几年持续热门的研究方向了吧。也可参考我的一个关于相关问题的回答:
为什么凸优化这么重要?
谢邀 @我是黑猫警长的幺崽崽 。前面几位说得挺好的了,我来说点自己的想法。首先说一下,这个问题是一个很大很深的topic,因为它涉及到机器学习和优化理论两方面的内容。所以每个人观点角度不同,看法也不尽相同,个人所知有限仅仅从自己所知道的一点谈一谈想法。
首先这个问题的角度实际上是说,优化能帮深度学习做什么?那么还有一个与之镜像的问题就是 深度学习能帮优化做什么?完整的来看这两个互为镜像的问题构成了 优化和深度学习的交叉研究。这里我们主要谈谈 优化能帮深度学习做什么?另外一个镜像问题可以参考【学界】深度学习如何影响运筹学?
Bottou L, Curtis F E, Nocedal J. Optimization methods for large-scale machine learning[J]. SIAM Review, 2018, 60(2): 223-311. 这本书是围绕随机梯度算法展开的(stochastic gradient method, SG),写得理论性和易读性兼具是一本不可多得的好书。前面有人已经做了详细介绍这块就不多说了。
这本书实际上是属于一个系列的 Foundations and Trends in Machine Learning 这个系列下面有很多本书,很多都是机器学习和优化理论的前沿交叉内容,除了上面那本我也推荐以下几本
1 Stephen Boyd 写的ADMM Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers
这本书也比较有名可能很多同学已经读过了。ADMM实际上比较老的一个方法,在机器学习一炮走红之后 ADMM又被人们重新关注。其基本思想还是用拉格朗日乘子法松弛优化问题的约束到目标函数上去,进而达到把大规模的优化问题拆分成子问题的目的。拆分之后的问题还非常适合分布式计算。
总结一下就是 如何利用优化理论的一些手段拆分问题,使得问题化繁为简还利于并行计算或者分布式计算。
2 Non-convex Optimization for Machine Learning
最近也是刚在看这本书,实际上有很多机器学习或者深度学习training 的model 并不是凸优化问题。所以Non-convex optimization 就显得比较重要了。传统的优化理论针对Non-convex optimization 主要有两种思想:1还是采用松弛的方法,把一些约束松弛掉,这样可以用convex 的去逼近non-convex的(可以看做是将non-convex 转化为convex的),2直接用non-convex 的一些 technique。
总结一下就是 深度学习的优化问题自然是Non-convex 的。那么如何用一些non-convex的方法去帮助深度学习优化问题的求解是关键。
3 Online Learning and Online Convex Optimization
Online learning 顾名思义,机器学习算法很多时候面对的是在线的问题,training set在不停的变化,数据在不停的在线的收集呢,此时就是一个Online的问题。因此这类机器学习模型的训练也就成了Online convex optimization。Online convex optimization的问题有两个要点:1 training set 变化了之后,如何利用以前的信息少计算一些;2 既然是online的问题,很可能对算法实时性要求更高。
目前想到的就这么几个点,比较粗略,比较泛泛而谈吧,欢迎各位留言交流哈。
从最开始的语义分割(纯CNN)
到最近几个月的半自动像素级别标注(带实习生延续做博士课题)
再到即将要做的AutoML、Meta Learning(优化算法选择CNN框架、超参学习等)
也算对优化理论和深度学习的交叉有点浅见
这里权当抛砖引玉
俩年前在 @运筹OR帷幄 专栏开篇文章中,我提到
【学界】人工智能的“引擎”--运筹学,一门建模、优化、决策的科学
深度学习里的损失函数,包含线性和ReLU等非线性函数,由于“深”,他们最终复合成一个极度非凸的函数。
例如h(x)=f(g(x))就是一个f和g复合函数。
深度学习中的“学习”一词,本质上便是通过大量标注的数据样本学习和计算最优参数的优化问题。
因此,优化理论的发展,对于深度学习的效率和精度尤为重要!
下面这本Fcebook AI、Lehigh Uni、Northwestern University合著的电子书是不错的参考:
https://leon.bottou.org/publications/pdf/tr-optml-2016.pdf深度学习的优化理论经过从SGD到Adagrad再到Adam,几经沉浮
但SGD(随机梯度下降算法,凸优化经典)却仍广泛使用
这方面的Paper太多,多发在NIPS、ICML等AI顶会上,就不一一列举了
下面这篇是不错的科普综述:
http://lipiji.com/docs/li2017optdl.pdf如果对于优化理论不是非常了解,下面这个暑期学校的ppt会是不错的入门:

深度学习一直以来被学术界认为是“黑箱子”
因为是一个超高维的非凸优化问题
加上(超)参数的数量非常多
例如:学习率、初始值、正则项、网络设置几层、模型怎么搭等等
因此深度学习的表现有非常大的“不可预见性”
深度学习从业者也经常被戏称为
优化理论却可以帮助深度学习
从前几年的超参数学习、优化参数的学习
Chapter 1: Hyperparameter Optimization. By Matthias Feurer and Frank Hutter
Chapter 2: Meta Learning By Joaquin Vanschoren
到近年的深度学习模型结构的学习
Chapter 3: Neural Architecture Search By Thomas Elsken, Jan-Hendrik Metzen and Frank Hutter
如Google Brain最近的NasNet
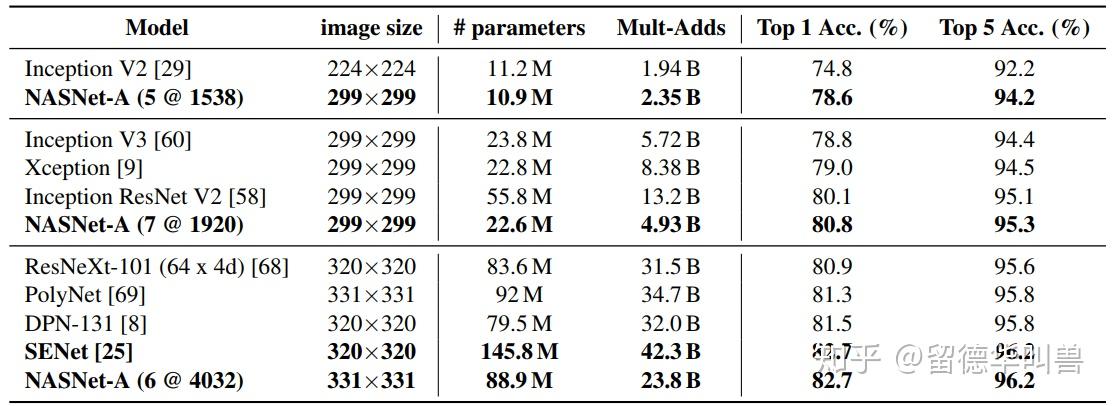
用AutoML学习得到的深度学习框架NasNet
在同等条件(模型参数和计算量)下
cnn模型所需的计算力(flops)和参数(parameters)数量是怎么计算的?
是非常有前景的学术研究方向
它们无不用到了
或强化学习、RNN等更"高级"的算法
【学界】整数规划精确算法/近似算法/(元)启发算法/神经网络反向传播等算法的区别与关联
这里推荐一个学术网页
上面汇总了几乎所有AutoML相关的开源书籍和论文
AutoML这也是我的博士课题之一
深度学习时代,对于高精度标注数据的需求日益剧增
公司最终的核心竞争力不在于CNN模型的优劣
以下图我目前的主要工作语义分割举例

深度学习的任务是将车载摄像头拍摄的图片中
而深度学习模型要有好的表现
就需要千万张这样人工标注好的像素级别的图片进行训练
(戴姆勒公司是目前行业的翘楚,公开了数个标准训练集)
据传,人工标注上图这样一张图片
这时候,就可以利用优化算法来加速标注的过程

以上是我博士期间设计的半自动标注优化算法
标注者可以用涂鸦的方式与图片交互
整数规划算法会给出“初步”的分割
如果觉得不满意
可以再次涂鸦或者用画笔“精修”边界的像素
如果一张语义分割标注数据价值10元人民币
每个汽车集团无人驾驶汽车要上路保守估计需要1000万张高精度的训练图片
如果我的算法可以使得标注效率提高哪怕10%
这方面的论文推荐俩篇(Kaiming He以及牛津Philip H.S. Torr组的最新成果):
ScribbleSup: Scribble-Supervised Convolutional Networks for Semantic Segmentationhttp://www.robots.ox.ac.uk/~tvg/publications/2018/0095.pdf此外,Automatic Annotation也是当前的研究热点。
由于篇幅原因
这里只列出以上3个优化理论在深度学习的应用方向
其他方向例如运筹学、优化理论在大规模集群运算中的算力和计算资源的调度问题
以及无人驾驶等深度学习应用场景中,各个感知模块存在倚赖关系的调度问题等等
它们本质其实都是运筹学中经典的调度问题
只是应用场景从供应链/交通/航空转到了深度学习
运筹OR帷幄:【无人驾驶】软件架构--基于AUTOSAR的多模块任务分配策略
以上
仅抛砖引玉
欢迎评论补充
也欢迎同行投稿至@运筹OR帷幄
加入20多个细分微信学术群学习和交流~
更新:
@运筹OR帷幄发布了该回答的扩充版本
优化 | 优化理论能给深度学习带来怎样的革命?并且整理了一大波相关学习资料(论文、数据、ppt等)
于公众号@运筹OR帷幄后台回复:
打包领取资料~
地址:海南省海口市玉沙路58号 电话:0898-88889999 手机:13988889999
Copyright © 2012-2018 天辰-天辰平台-天辰中国加盟站 ICP备案编:琼ICP备88889999号